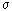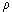| A | m2 | Cross sectional of the core plug |
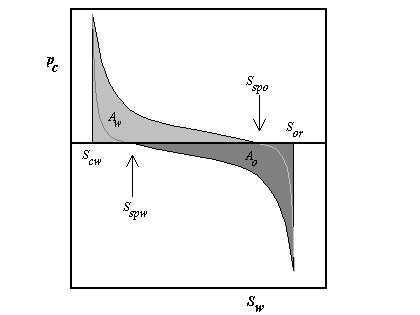
| Ao | Pa | Area under the imbibition pc-curve between Sspw and 1-Sor |
| Aw | Pa | Area under the imbibition pc-curve between Sspo and Scw |
| Io | | Amott index for oil |
| Iw | | Amott index for water |
| g | m/s2 | Centrifugal acceleration |
| K | m2 | Permeability |
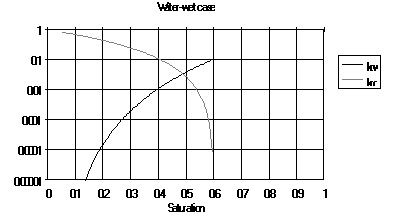
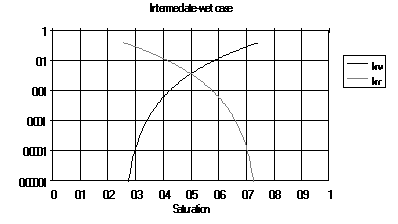
| kri | | Relative permeability for phase i |
| kro | | Relative oil permeability |
| kro,cw | | Relative oil permeability at connate water saturation |
| krw | | Relative water permeability |
| krw,or | | Relative water permeability at residual oil saturation |
| L | m | Length |
| M | | End-point mobility ratio |
| Ms | | Shock front mobility ratio |
| no | | Corey exponent for oil |
| nw | | Corey exponent for water |
| Nb | | Bond number |
| Nc | | Capillary number |
| pc | Pa | Capillary pressure |
| po | Pa | Oil pressure |
| pw | Pa | Water pressure, wetting-phase pressure |
| pnw | Pa | Non-wetting phase pressure |
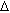 P P | Pa | Pressure difference |
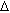 pi pi | Pa | Pressure difference in phase i |
| q | m3/s | Flow rate |
| qi | m3/s | Flow rate in phase i |
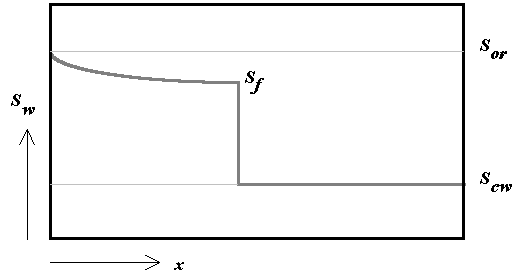
| Sw | | Water saturation |
| So | | Oil saturation |
| Sf | | Shock front saturation |
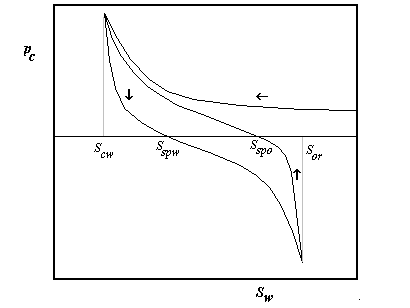
| Scw | | Connate water saturation |
| Sor | | Residual oil saturation |
| Sspo | | Spontaneous oil imbibition saturation |
| Sspw | | Spontaneous water imbibition saturation |
| S1,23 | Pa.m | Spreading coefficient of fluid 1 in between fluids 2 and 3 |
| U | | USBM wettability index |
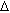 | | difference indicator |
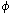 | | Porosity |
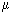 | Pa.s | Viscosity |
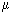 i i | Pa.s | Viscosity of phase i |
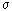 | Pa.m | Interfacial tension |
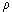 | kg/m3 | Density |
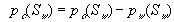 (1)
(1)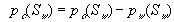 (1)
(1)
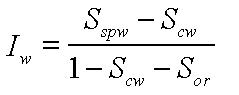 (2)
(2)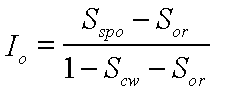 (3)
(3)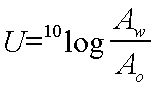
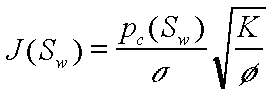 (4)
(4)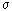 the interfacial tension between the two phases and
the interfacial tension between the two phases and 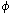 the porosity of the rock.
the porosity of the rock.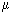 , which is forced to flow, at flow rate q, through a porous medium, of length L and with cross section A, such that the pressure difference across the length of the porous medium is
, which is forced to flow, at flow rate q, through a porous medium, of length L and with cross section A, such that the pressure difference across the length of the porous medium is 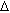 P. Then the permeability K of the material is defined as:
P. Then the permeability K of the material is defined as: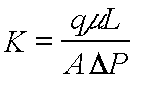 (5)
(5)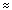 (1
(1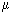 m)2 = 10-12 m2.
m)2 = 10-12 m2.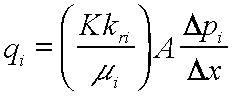 (6)
(6)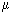 i the viscosity of phase i and
i the viscosity of phase i and 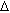 pi the pressure drop within phase i. The term in brackets is denoted the "mobility" of phase i.
pi the pressure drop within phase i. The term in brackets is denoted the "mobility" of phase i.
 10 mN/m or more), this is a good approximation.
10 mN/m or more), this is a good approximation.
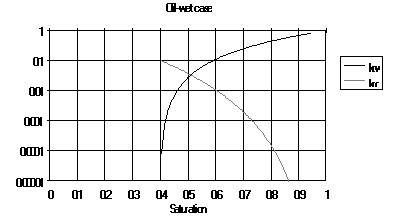
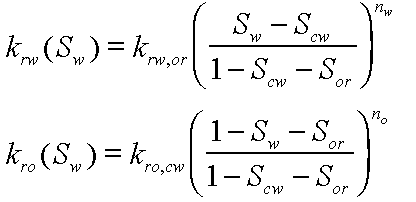 (7)
(7)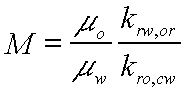 (8)
(8)
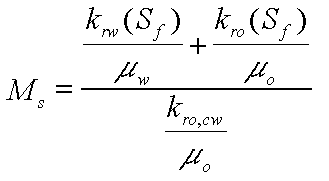 (9)
(9)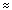 50 !
50 !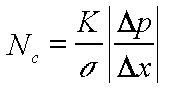 (10)
(10)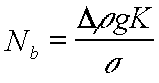 (11)
(11)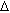 P
P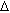 pi
pi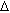
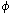
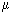
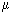 i
i